Hamilton Khaki X-Wind. Мини-обзор и первые впечатления

[mpoteychuk]

Сообщение от Mystic Traveller

Вопрос по X-Wind:

Там постоянно "тикает" маленькая секундная стрелка справа?
Центральная только при запуске хрона?

Именно так.

[booBot]

Вот шкала приспособы (Jeppersen's CR-3), которую пытались втиснуть в эти часы.
Неудивительно, что TS'у (и подключившемуся Lexey273'ю) не удалось разобраться, как этим хозяйством пользоваться.

Вычисление угла коррекции ветра - не все задачи, которые приходится решать штурману на CR-3. Определив величину угла, надо вычислить и скорость относительно земли, так как именно от неё зависит время прибытия в пункт назначения. Шаги по вычислению скорости не менее замысловаты, чем само определение угла коррекции.

Странно, что американская часовая фирма выбрала не самый популярный (среди американских же военных лётчиков) тип "компьютера". Большинство американских штурманов предпочитает более простые и ясные в обращении "компьютеры" - MB-2A или MB-9. Ими действительно можно пользоваться одной рукой, не требуется координатная сетка, по которой на CR-3 надо разбивать вектор скорости на две составляющие ("попутную" и "поперечную"), что не только облегчает ход решения, но и повышает его точность.

При некотором навыке - и на CR-3 можно делать вычисления как на MB-2A, но будет мешать участок шкалы со значениями косинусов (слева от красного треугольничка), перебивающий конец шкалы синусов.

[mpoteychuk]

О, спасибо за интересные факты.

Я полагаю что вряд ли кому то придет в голову действительно рассчитывать по этим часам угол коррекции ветра.
Скорее всего дизайнеры при разработке модели выбирали из всех возможных "калькуляторов" не по принципу чтобы летчикам было удобнее высчитывать корректировку скорости, а просто какой из них можно втиснуть на циферблат без ущерба для остальных функций а также какая из них будет лучше всего смотреться.

Когда то у Хамильтонов была модель Navy Regatta - такой же корпус, такой же механизм, только с уклоном в морскую тематику. Так вот там ради некоторых морских функций пожертвовали минутной стрелкой хронографа.

[booBot]

Строго говоря, нет разницы между "авиационными" и "лодочными" вычислениями - все штурманы решают одни и те же задачи. У моряков их даже больше - кроме угла сноса ветром, надо ещё вычислить угол сноса течением. Процедура одна и та же (только цена деления шкалы не "сотни" а "единицы" узлов).

Показанная вами Khaki Navy Regatta "заточена" под парусные обстоятельства, да ещё и гоночные.
Из этих двух моделей - я бы выбрал X-Wind, так как их логарифмической шкалой можно (при некотором навыке) и в продовольственном магазине пользоваться (для определения, например, килограммовой цены товара по стоимости некоторого его количества). Но на каком-нибудь Citizen Skyhawk'е логарифмическая линейка для магазинных подсчётов будет ГОРАЗДО удобнее, так как она для арифметики спроектирована (а не для тригонометрии).

[booBot]

Чтобы окончательно всё прояснить (или запутать?), вот инструкции к "полётным калькуляторам":

1. CR-3
2. MB-2A

[booBot]

Итого, чтобы никто не мог сказать, что Khaki X-Wind - это просто бижутерия, вот инструкция по вычислению угла коррекции ветра и скорости относительно земли.
Будем решать задачу по условиям, приведённым в Instruction Manual'е к часам, но по правильной методике, применяемой на калькуляторах типа MB-2A:

1. TC (true course, истинный курс самолёта) = 40°
2. WD (wind direction, направление ветра) = 70°
3. TAS (true airspeed, воздушная скорость) = 180kn
4. WS (wind speed, скорость ветра) = 40kn

.

Вычисление WCA (wind correction angle, "crab" angle, угол коррекции сноса):

1. 1) по схеме из главы 5 Инструкции, определим RWA (relative wind angle, курсовой угол ветра), RWA = WD-TC = 70°-40° = 30°,
2. 2) найдём на наружном безеле значение TAS=180kn, обозначаемое меткой "18"
3. 3) с помощью ЗГ "B" подведём к метке TAS ("18" на наружном безеле) вычисленное значение RWA=30°, находящееся на "C" - шкале синуов. НЕ ПЕРЕПУТАЙТЕ ЗНАЧЕНИЯ ШКАЛЫ СИНУСОВ СО ЗНАЧЕНИЯМИ УЧАСТКА ШКАЛЫ КОСИНУСОВ! (участок шкалы косинусов, значения от 15° до 45°, находится слева от окошка "E"). Если требуются углы RWA от 45° до 90°, то используем метки участка шкалы косинусов: sin(45°)=cos(45°), sin(50°)=cos(40°), sin(55°)=cos(35°), sin(60°)=cos(30°), sin(65°)=cos(25°), sin(70°)=cos(20°), sin(75°)=cos(15°).
4. 4) ни безель, ни шкалу синусов больше не вращаем
5. 5) находим на наружном безеле значение WS=40kn, обозначаемое меткой "40", и напротив метки "40" наружного безеля читаем на шкале синусов значение WCA, оно оказывается равным 6,5°
6. 6) смотрим на векторную диаграмму (или левый рисунок главы 5 Инструкции), определяем, что ветер встречный, с правого борта. Доворачиваем самолёт вправо на 6,5°, к ветру. Нос самолёта теперь указывает в направлении TH=TC+WCA=46,5°, которое можно "запомнить" в окошке "E" на шкале "нижнего" внутренного безеля, повернув его с помощью ЗГ "D".

Самолёт теперь летит боком, (делает "crabbing"), но относительно земли держит курс, равный TC (true course), то есть - на пункт назначения.
На компасе мы видим значение TH (true heading), туда повёрнут нос самолёта.
Теперь надо определить скорость самолёта относительно земли.

Вычисление GS (ground speed, скорость относительно земли):

1. 1) ни безели, ни шкалу синусов не вращаем! Их положения соответствуют только что решённому шагу (определения WCA)
2. 2) вспомогательный угол, требующийся для вычисления GS, показан на векторной диаграмме красным, вычисляется по правилу: RWA+WCA в попутном ветре, RWA-WCA во встречном ветре. По условиям задачи - ветер встречный, вычисляем значение вспомогательного угла RWA-WCA=30°-6,5°=23,5°
3. 3) находим на шкале синусов это значение, "23,5°"
4. 4) напротив него - считываем значение GS (ground speed, скорость относительно земли) на наружном безеле, она оказывается равной 144 узла.

Готово!

Если бы на часах была ещё одна числовая логарифмическая шкала, мы смогли бы вычислить и время полёта, разделив расстояние до пункта назначения на только что полученное значение GS. Но увы, тут нам X-Wind не поможет, так как всё-таки является бижутерией!
Наверное можно как-то исхитриться, запомнить расположение делений на всех шкалах, совместить метку, соответсвующую длине пути на наружном безеле, с меткой, соответствующей скорости на шкале углов, и прочитать результат. Но без часов я проделать это "в уме" не могу.
Если кто-нибудь сфотографирует свой X-Wind в положении решения вышеупомянутой задачи, я попробую придумать дальнейшие действия.

Итак, напомню схему решения задачи:

1. 1) определяем курсовой угол ветра (RWA) по значениям TC и WD (см. рис. к главе 5)
2. 2) совмещаем значение TAS с меткой RWA, находим метку WS - под ней считываем значеие WCA, в зависимости от направления ветра (попутный/встречный) складываем или вычитаем значения углов RWA и WCA, над результирующим (суммарным или разностным) значением угла считываем величину GS

Всё решается единственным поворотом безеля.

Всем спасибо за внимание.
Сам получил удовольствие, разбираясь со шкалами этих часов.


PS
Домашнее задание
Вычислить WCA и GS для второй и третьей иллюстрации главы 5 Инструкции к часам.
Считаем скорости ветра и самолёта теми же: WS=40kn, TAS=180kn.


PS2
Пока Hamilton не сделает правильные шкалы (и нормальный 24-часовой циферблат!) - покупать эти часы не буду.

Чтобы превратить эту имитацию CR-3 в имитацию MB-2A, надо:

1. 1) добавить равномерную шкалу 0°~359° на наружный безель; исправить разметку "нижнего" внутреннего безеля, сделав на ней четыре сектора по 90°: (0°, 10°...80°, 90°, 80°...10°, 0°, 10°...80°, 90°, 80°...10°, 0°), чтобы облегчить шаг вычисления RWA
2. 2) убрать участок шкалы косинусов, достроить там хвост шкалы синусов
3. 3) (наверняка нереализуемо) добавить на безель "C" логарифмическую числовую шкалу
4. 4) если без второй логарифмической шкалы - придумать способ деления чисел на имеющихся шкалах (например - относительно метки "12 часов")

В противном случае придётся носить вторые часы, типа Citizen Skyhawk, для продолжения рассчётов времени и расхода топлива.

[Lexey273]

Сообщение от booBot

Итого, чтобы никто не мог сказать, что Khaki X-Wind - это просто бижутерия, вот инструкция по вычислению угла коррекции ветра и скорости относительно земли.
Будем решать задачу по условиям, приведённым в Instruction Manual'е к часам, но по правильной методике, применяемой на калькуляторах типа MB-2A:

Интересно, посмотрю на досуге. Получается, в инструкции к часам зачем-то приведены избыточные действия (напр., использование графика на прилагаемой пластиковой карте)..

Сообщение от booBot

Чтобы окончательно всё прояснить (или запутать?), вот инструкции к "полётным калькуляторам":

1. CR-3
2. MB-2A

Ну почему же запутать, по этим мануалам и разбирался 4 года назад
А претензии были к пробелам в инструкции часов. Видимо, не хотели слишком усложнять - и эту то никто не читает. И скрытый безель 360 градусов - тут чисто дизайнерский элемент. Для сохранения вычисленного угла не очень удобен (если угол равен 5, 10, 15 и т.д. градусов, то окошко будет пустым). Но смотрится эффектно. Также, элементом дизайна можно считать возможность вращения внутреннего безеля с синусами (для нужного совмещения дисков достаточно поворотного внешнего). Вобщем, согласен, что

Сообщение от mpoteychuk

Скорее всего дизайнеры при разработке модели выбирали из всех возможных "калькуляторов" не по принципу чтобы летчикам было удобнее высчитывать корректировку скорости, а просто какой из них можно втиснуть на циферблат без ущерба для остальных функций а также какая из них будет лучше всего смотреться.

Что им и удалось - часы выглядят достаточно гармонично, даже ощущения перегруженности не возникает, как со многими другими пилотскими часами (теми же Citizen, например).

Вообще, мне лично было интереснее понять какие действия производятся данным калькулятором (применение в авиации, лишь частный случай). Их можно сформулировать довольно кратко: мгновенное вычисление синуса и косинуса любого угла, умноженного на любое число (подробнее было тут ).

За проделанную работу и подробное описание (тем более, даже не собираясь покупать часы) спасибо! Фото с положением безеля, как в задаче выложу.

P.S. И ещё, не понял, как это

Сообщение от booBot

4) если без второй логарифмической шкалы - придумать способ деления чисел на имеющихся шкалах (например - относительно метки "12 часов")

?

[booBot]

Я не знаю, о чём думал[а девочка-]дизайнер, но если бы стояла задача сделать не бижутерию, а действительно полезный в экстренной ситуации "полётный калькулятор" на часах - выбрали бы набор шкал MB-2A. Разумеется - если бы про него знали, в чём есть сомнения.

А так - получилась загадочная игрушка, к коротой они не смогли даже инструкцию целиком сделать. Значением угла коррекции сноса навигация не оканчивается. Согласен, что неподготовленный человек, увидев все эти шкалы/безели, прилагаемую координатную карточку, - думает: "Во! Крутейшая вестчь!".
Однако, я полагаю, у многих будет формироваться неудовлетворённость, что они не смогли разобраться с часами... И этот "осадочек" будет относиться ко всей марке (Hamilton) в целом, маркетинговый минус, я считаю.

К вашему недоумению касательно №4: на обычной лог-линейке есть числовая шкала на неподвижной части, есть вторая числовая шкала на движке. Совмещая деления этих шкал - можно производить операции умножения и деления соответствующих чисел.
На данных часах есть одна числовая шкала (на наружном безеле), и есть шкала синусов. В результате - мы можем (если без ухищрений) умножать и делить только числа и значения синусов. Разделить 520 на 144 сразу не получится.
Я тут на выходных прикидывал так и сяк, единственный способ (до которого я додумался) вычислить значение дроби 520/144 - это совместить "начало шкалы" безеля (метку "10") с началом шкалы синусов (красным треугольником), запомнить значение угла, напротив которого окажется деление "144". Потом к этому значению подвести метку "52" безеля - и напротив красного треугольника считать результат на безеле.
Требуется одно дополнительное движение, теряется точность.
Про "12 часов" - это был наобум взятый (неправильный) вариант подхода к делению в условиях отсутсвия необходимой шкалы.

[Lexey273]

Сообщение от booBot

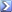
Если кто-нибудь сфотографирует свой X-Wind в положении решения вышеупомянутой задачи, я попробую придумать дальнейшие действия.)

Не знаю, нужно ли ещё, но вот (здесь и далее прошу прощения за качество картинок, фото телефоном):

Сообщение от booBot

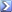
Чтобы превратить эту имитацию CR-3 в имитацию MB-2A, надо:

1. 1) добавить равномерную шкалу 0°~359° на наружный безель; исправить разметку "нижнего" внутреннего безеля, сделав на ней четыре сектора по 90°: (0°, 10°...80°, 90°, 80°...10°, 0°, 10°...80°, 90°, 80°...10°, 0°), чтобы облегчить шаг вычисления RWA
2. 2) убрать участок шкалы косинусов, достроить там хвост шкалы синусов
3. 3) (наверняка нереализуемо) добавить на безель "C" логарифмическую числовую шкалу
4. 4) если без второй логарифмической шкалы - придумать способ деления чисел на имеющихся шкалах (например - относительно метки "12 часов")

В противном случае придётся носить вторые часы, типа Citizen Skyhawk, для продолжения рассчётов времени и расхода топлива.

Так же, как в комплект к Skyhawk, пришлось бы носить X-Wind (для начала расчётов)
Нельзя объять необъятное ©. Конечно, можно добавить ещё две шкалы – но тогда придётся пожертвовать, собственно, часами (как аксессуаром для повседневной жизни), поскольку смотреться будет совсем по-фриковски. Да и, к тому же всегда что-то останется неохваченным – как пример, в том же CR-3 есть ещё диск для расчёта реальной высоты по барометрическому давлению с поправкой на текущую температуру..

Сообщение от booBot

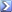
Я не знаю, о чём думал[а девочка-]дизайнер, но если бы стояла задача сделать не бижутерию, а действительно полезный в экстренной ситуации "полётный калькулятор" на часах - выбрали бы набор шкал MB-2A. Разумеется - если бы про него знали, в чём есть сомнения.

А так - получилась загадочная игрушка, к коротой они не смогли даже инструкцию целиком сделать. Значением угла коррекции сноса навигация не оканчивается. Согласен, что неподготовленный человек, увидев все эти шкалы/безели, прилагаемую координатную карточку, - думает: "Во! Крутейшая вестчь!".
Однако, я полагаю, у многих будет формироваться неудовлетворённость, что они не смогли разобраться с часами... И этот "осадочек" будет относиться ко всей марке (Hamilton) в целом, маркетинговый минус, я считаю.

Я не пилот, конечно (скорее уж математик ), но, насколько понимаю, если говорить о воображаемой «экстренной ситуации» (в самолёте сломаны/отсутствуют навигационные приборы), всё же главное - правильно вычислить направление, куда лететь (тот самый угол коррекции сноса), тогда хотя бы есть шанс .
А так да, игрушка, конечно, кто ж спорит. Как и многое другое в часах вообще – взять хоть те же гелиевые клапаны в дайверах. К слову, «загадочные игрушки», которые работают, но не сразу понятно как – нмв, самые интересные. Так что изъяны инструкции, думаю, не сильно большая беда – так, квест дополнительный. Вот если бы какой-нибудь из безелей люфтил, или с разметкой накосячили – это было бы действительно обидно.
----------------------------------------------

Теперь по поводу логарифмической линейки.
Тут уж получается в любом случае, или на внутреннем безеле шкала синусов, или логарифмическая линейка.. Сегодня пришла мысль, что могли бы её на скрытый безель нанести вместо непонятной шкалы 0°~359°. Но тогда пришлось бы крутить безель синусов, чтобы найти на ней нужное значение (когда уже выставлено нужное соответствие).

Сообщение от booBot

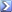
Я тут на выходных прикидывал так и сяк, единственный способ (до которого я додумался) вычислить значение дроби 520/144 - это совместить "начало шкалы" безеля (метку "10") с началом шкалы синусов (красным треугольником), запомнить значение угла, напротив которого окажется деление "144". Потом к этому значению подвести метку "52" безеля - и напротив красного треугольника считать результат на безеле.
Требуется одно дополнительное движение, теряется точность.

Да, интересный подход, мне такое в голову не пришло. Для приближённых вычислений я пользовался способом, который описывал по ссылкам выше, а именно, использовал свойство sinX->X для малых углов - т.е. шкалу для малых углов (которая на внутреннем безеле ближе к центру, для углов < 20° совпадает с основной шкалой) можно рассматривать, как ответную часть (логарифмической линейки) к внешнему безелю. Действительно, если совместить 10 на внешнем безеле и 1° на внутреннем, то увидим, что шкалы безелей почти совпадают (до 20° смотрим на основную шкалу, далее – на шкалу для малых углов (умножая их на 10, конечно)). Вот, примерно так:


Для вашего примера деления 520 / 144 выставляем 14,4 на внешнем безеле напротив 1° на внутреннем, и, напротив 52 на внешнем, на внутреннем читаем результат ~3,7 (или даже чуть меньше), что не очень сильно отличается от правильного (3,6(1)). Вот так это выглядит:

[booBot]

Я в кармане рубашки всегда ношу 12-см лог.линейку.

Как-то раз, в перелёте HEL-SIN попробовал вычислить дальность по теореме косинусов (на этой линейке), к моему удивлению результат отличался от "калькуляторного" (на Casio fx-300ES Plus) всего на ~70 морских миль.

Одно дело, когда "не сразу понятно", как работает игрушка, и совсем другое - когда Инструкция обрывается на полушаге решения. Для шкал MB-2A инструкция была бы в разы проще и понятнее.
А про остальные шкалы (коррекции TAS и высоты) - что жалеть? Надо сперва за штурвал как-то умудриться попасть!